JournalofChongqingUniversityofTechnology（NaturalScience）2022年第36卷第7期Vol．36No．72022收稿日期：2021－09－26基金项目：五凌电力有限公司综合智慧能源业务及数字化建设发展规划项目（320115JX0120210002）作者简介：刘晨，男，硕士，经济师，主要从事综合能源服务、电力数字孪生技术、新能源技术研究，E-mail：1071617197@qq．com；通讯作者龙浩，男，工程师，主要从事综合智慧能源、电力市场营销研究，E-mail：973594826@qq．com。本文引用格式：刘晨，龙浩，张文栋，等．综合能源系统多能互补优化方法研究［J］．重庆理工大学学报（自然科学），2022，36（7）：264－271．Citationformat：LIUChen，LONGHao，ZHANGWendong，etal．Ｒesearchonmulti-energycomplementaryoptimizationmethodofintegratedenergysystem［J］．JournalofChongqingUniversityofTechnology（NaturalScience），2022，36（7）：264－271．doi：10．3969/j．issn．1674－8425（z）．2022．07．033综合能源系统多能互补优化方法研究刘晨1，龙浩1，张文栋1，黄蒙2（1．五凌电力有限公司，长沙410000；2．山东电力工程咨询院有限公司，济南250000）摘要：针对我国的能源体系结构存在着功能效率低下、能源搭配不当、环境污染严重等问题，采用博弈论理念实现综合能源系统多能互补优化调度，优化了传统的能源协同调度问题。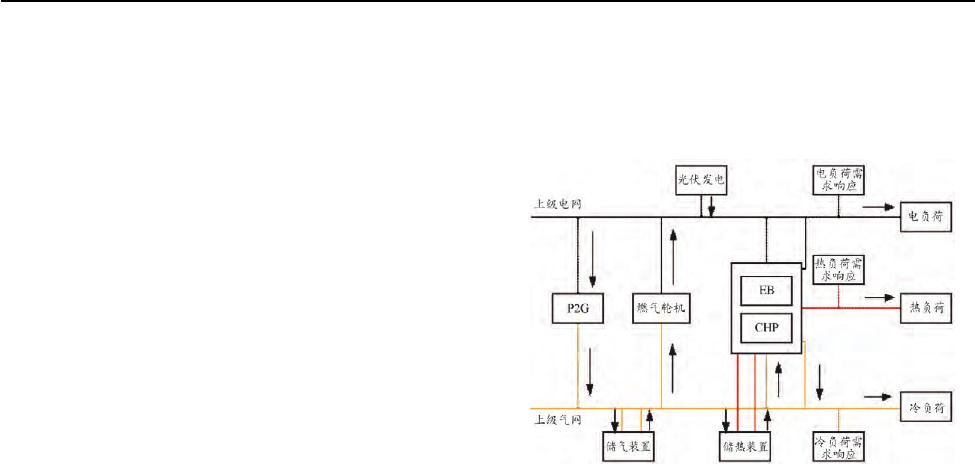该综合能源多能互补优化调度模型由热电联产机组、光伏发电和电网组成，分别建立了非合作博弈和合作博弈模型来求解系统的最大收益，分别比较了在非合作、部分合作和完全合作这3种博弈模式下的系统总收益。根据参与者是否结盟，提出5种博弈模式来证明Nash均衡，并通过仿真实验得到各模式下的Nash均衡策略。仿真结果表明，与非合作博弈相比，其余合作博弈产生的价值均大于非合作博弈，在完全合作博弈模式下的系统总利润率是最大的。验证了只有参与者完全进行合作才能满足保证多能互补能源系统利润最大化。关键词：博弈论；综合能源系统；Nash均衡；合作博弈；非合作博弈中图分类号：TP181文献标识码：A文章编号：1674－8425（2022）07－0264－080引言在综合能源系统的研究中，目标是在多种能源之间实现优势互补和能源的分级利用，提高能源的复用率，实现节能低碳的目标［1－2］。在多能互补协同调度方面，文献［3－4］在综合能源系统中同时接入了天然气、热电、风机和光伏发电，构建了经济调度模型，并制定了优化策略，降低了综合能源系统成本。在综合能源系统的能量流模型方面，文献［5］在关于电气能流模型的研究中，采用电转气和燃气轮机2个耦合设备进行能量转换，在电气综合能源系统中将全局搜索能力与局部搜索能力进行结合，从而来验证该混合算法的可行性和可靠性。在储能装置方面，储能是综合能源系统中重要的一个单元，储能的存在极大地提升了可再生能源的消纳能力，将多余的能量进行储存［6］。文献［7］对风电、热电集中消纳，极大地提升了能源系统的自我调节能力和灵活性。在系统接入可再生能源方面，文献［8－9］建立了源－网－荷全过程的不确定性的分析框架，重点分析了风力发电、光伏发电和水力发电的不确定性及其对系统的影响。对于不同模型的求解问题，文献［10－14］将混合整数线性法和动态规划法进行融合来研究电－冷－热联产系统中的电热协同调度问题；文献［15］建立了基于热力学原理的电－冷－热优化模型，解决了园区热力系统问题。上述的文献主要规划了能源站内的设备容量，设计了多能互补综合能源系统规划设计框架和经济模型，但是却未能具体说明所提出的模型框架在达到什么阶段才能保证多方利益最大化以及各类负荷的供需平衡。针对上述文献存在的不足之处，主要贡献如下：1）将经济学中的博弈论思想引入综合能源系统的研究领域，将能源系统中的所有设备作为博弈参与者来构建模型；2）分析比较合作和非合作2种博弈模式下的结果；3）通过分析Nash均衡结果，进一步验证最优策略下的供需平衡。1博弈模型设计将博弈论思想与多能互补综合能源系统进行融合建模，模型建立的思路为：在Nash均衡模式下，综合能源系统的不同设备作为参与者，参与者会寻找博弈的均衡点。在Nash均衡点上，参与者都不会私自的改变策略，这时，每个参与者的利益将会最大化［16］。1．1多能互补综合能源系统架构模型多能互补综合能源系统由热电联产（com-binedheatingandpower，CHP）机组［17］、光伏发电（photovoltaic，PV）和电网构成，如图1所示。综合能源服务商配置光伏发电、热电联产、燃气轮机等设备来满足用户对用能的需求，热电联产设备和电锅炉（electricboiler，EB）设备利用储热装置提供的热源产生热电荷，而发电余热会经由换热器结合热泵满足用户对热负荷的需求。1．2博弈要素分析博弈者可以通过博弈来争夺自身利益的最大化［18］。由博弈理论定义可知，博弈的条件包括：多个参与者、参与者自己的策略和参与者庞大的信息储备等要素［19］。图1多能互补综合能源系统结构示意图1．2．1博弈参与者集合博弈参与者集合分别是热电联产、光伏、电网，可以用C、Ｒ、E表示，记博弈参与者集合为：N=｛C，Ｒ，E｝（1）1．2．2博弈参与者的策略集合参与者的策略集合包括热电联产、光伏和电网的装机容量，分别记为HC、HＲ、HE，即：HC∈ΩC=｛HminC，HmaxC｝（2）HＲ∈ΩＲ=｛HminＲ，HmaxＲ｝（3）HE∈ΩE=｛HminE，HmaxE｝（4）其中：Hmini、Hmaxi指的是参与者集合的最小下限和最大上限。因此，博弈的策略集合为Ω=｛ΩC，ΩＲ，ΩE｝。1．2．3博弈参与者的收益参与者收益定义为年总收入与总成本之差，记为IC、IＲ、IE，收益向量为：I=（IC，IＲ，IE）（5）参与者i（C，E，Ｒ）的收入包括出售电负荷收入IEiSEL、出售热负荷收入IHiSEL、出售冷负荷收入ICiSEL和报废收入IiD等。以参与者C为例，出售电负荷收入如式（6）所示：IECSEL=·PECSELＲE（6）式中：ＲE表示电价，元/（kW·h）；PECSEL表示热电联产出售电量，kW·h。562刘晨，等：综合能源系统多能互补优化方法研究出售热负荷、冷负荷收入如式（7）和式（8）所示：IHCSEL=PHCSELＲH（7）ICCSEL=PCCSELＲC（8）式中：ＲH、ＲC分别表示出售热负荷和冷负荷的价格，元/（kW·h）。由于全国各地出行政策不同，所以对综合能源系统补贴各不相同。补贴收入ICSUB会自动根据售电量进行补贴，如式（9）所示：ICSUB=PECSELＲSUB（9）式中：ＲSUB为售电补贴，元/（kW·h）。参与者的设备年报废收入如式（10）所示：ICD·=ECDCγ（1+γ）LC－1（10）式中：EC为热电联产容量；DC为热电联产报废收入，元/kW；γ和LC分别为年收益率和热电联产设备寿命。热电联产设备的年投资费用为：CCINV=ECUC（1+γ）LC（1+γ）LC－1（11）式中：UC为热电联产单位功率造价，元/kW；CCINV表示年折算设备投资费用。热电联产设备所需要的燃料费用为CCF，如式（12）所示：CCF=∑m∑hQCm，h·V·Pgas·dm（12）式中：m和h分别表示月份、小时；QCm，h、V、Pgas分别表示热电联产供电功率、热电联产设备气耗率、天然气价格，元/Nm3。参与者C的维护费用如式（13）所示：CCOM=∑m∑hQCm，h·MC·dm（13）式中：MC为热电联产设备执行系数，元/（kW·h）。综上所述，参与者i的年收益如式（14）所示：Ii=IEiSEL+IHiSEL+ICiSEL+IiSUB+IiD－CiINV－CiF－CiOM（14）1．2．4均衡参与者的集合、参与者的策略集合和参与者的总体收益经过博弈后会达到Nash均衡，可表示为（HC，HＲ，HE），此时综合能源系统的收益最大。1．3系统能量平衡约束1．3．1电、热、冷平衡约束电功率平衡约束：∑jledt，i=Pt，j，gt+·Pt，j，pv－·Pt，j，ec－·Pt，j，hp+Pdisct，j，e·－·Pcht，j，e+Pbuyt，j·－·Psellt，j+∑k（qendt，e，kj·－·qstartt，e，jk）（15）热功率平衡约束：∑jlhdt，i·=ht，j，gt+ht，j，gb－ht，j，ac+ht，j，hp+Pdisct，j，h－Pcht，j，h+∑k（qendt，h，kj－·qstartt，h，jk）（16）冷功率平衡约束：∑jlcdt，i=ct，j，ec+ct，j，hp+ct，j，ac（17）式中：lhdt，i和lcdt，i表示负荷i的热、冷负荷；Pt，j，s，ct，j，s和ht，j，s表示s设备所产生和消耗的电、冷、热功率；下标s=｛gt，ec，hp，gb，pv，ac｝，分别对应设备GT，EC，HP，GB，PV，AC。1．3．2热电联产输出热电联产设备的热、电输出关系如下式所示：0≥∑jlCdt，i≤HC（18）Hht，j，gt+Hct，j，ec=∑jlcdt，iλ（19）0≤Pdisct，j，e≤HＲ（20）0≤Pcht，j，e≤HE（21）式中：λ为热电联产机组的热电比。2基于博弈论的多能互补综合能源设计模型在多能互补综合能源设计模型中，热电联产［20］、光伏［21］、电网有多种博弈模式：三者都是合作博弈、两者是合作博弈和三者都不合作博弈［22］，如表1所示。2．1非合作博弈模型综合能源系统中的非合作博弈是指参与者只会追求本身利益，而不会去考虑整个系统的总体收益。因此，该系统形成的非合作博弈模型如下。662表1综合能源系统博弈模式编号博弈模式含义合作程度1｛C｝，｛Ｒ｝，｛E｝热电联产、光伏、电网都不合作非合作2｛C，Ｒ｝，｛E｝热电联产、光伏合作，电网独立决策部分合作3｛C，E｝，｛Ｒ｝热电联产、电网合作，光伏发电独立决策部分合作4｛Ｒ，E｝，｛C｝光伏、电网合作，热电联产独立决策部分合作5｛C，Ｒ，E｝热电联产、光伏、电网合作完全合作1）参与者集合N=｛C，Ｒ，E｝（22）2）参与者策略集合Ω=｛ΩC，ΩＲ，ΩE｝（23）3）参与者收益函数IC（HC，HＲ，HE）IＲ（HC，HＲ，HE）IE（HC，HＲ，HE{）（24）根据Nash均衡定义，模型中的Nash均衡点（HC，HＲ，HE）满足：HC=·arg·HCmax（HC，HＲ，HE）（25）HＲ=·arg·HＲmax（HC，HＲ，HE）（26）HE=arg·HCmax（HC，HＲ，HE）（27）由上式可知，热电联产、光伏、电网经过多次博弈后，最终可以得到Nash均衡的最优解，保证了参与者利益最大化的同时效率也最大化。2．2合作博弈模型合作博弈主旨是研究参与者之间的利益分配问题，合作博弈有助于提高整个系统的收益［17］。1）参与者集合N=｛C，Ｒ，E｝（28）2）参与者策略集合ΩＲE=｛HminＲ，HmaxＲ，HminE，HmaxE｝ΩC=｛HminC，HmaxC｝（29）3）参与者收益函数IＲE（HC，HＲ，HE），IC（HC，HＲ，HE）（30）根据Nash均衡定义，模型中的Nash均衡点（H'Ｒ，H'E）和H'C满足：（H'Ｒ，H'E）=argHＲ，HEmaxIＲE（H'C，HＲ，HE）（31）H'C=argHCmaxIC（HC，H'Ｒ，H'E）（32）与非合作博弈均衡解类似，（H'Ｒ，H'E）和H'C经过多次博弈，最终可以得到Nash均衡的最优解，保证热电联产、光伏、电网联盟在获得最大收益的同时，也可以提高参与者的效率。3Nash均衡证明和系统模型求解3．1Nash均衡存在性证明Nash均衡存在性定理指出，对策略式博弈G=｛N；S1，…，Si，…，Sn；u1，…，ui，…，un｝，若集合Si为紧凸集，ui是连续的，且关于Si拟凹，则存在Nash均衡［23］。由定义，∃函数f（x），若∀x1，x2∈U，∀r∈（0，1），有f［rx1+（1－r）x2］≥rf（x1）+（1－r）f（x2），则称f（x）在区间U是凹函数［24－25］。在合作博弈模式下，IC是HC的凹函数，系统收益IＲE的凹凸性由HＲ和HE两个变量决定［26］。3．2综合能源系统模型求解策略非合作博弈模式下参与者会追求最大化的利益，而不会去考虑整个系统的总体收益。合作博弈指参与者不会单纯地考虑自身的利益，而是尽量保证系统总体的收益。各变量将会随机选取数值作为初始博弈均衡点，以表1中的部分合作博弈（｛C｝，｛Ｒ，E｝）和完全合作博弈｛C，Ｒ，E｝为例，第k轮结果由第k－1轮结果通过迭代得到，部分合作博弈记为［（HＲ，k，HE，k），HC，k］，即：（HＲ，k，HE，k）=argHＲ，HEmaxIＲE（HC，HＲ，k－1，HE，k－1）（33）HC，k=argHCmaxIC（HC，k－1，HＲ，HE）（34）完全合作博弈｛C，Ｒ，E｝，记为（HＲ，k，HE，k，HC，k），即：（HＲ，k，HE，k，HC，k）=argHC，HＲ，HEmaxICＲE（HC，k－1，HＲ，k－1，HE，k－1）（35）最后，在相邻两次求解完成之后，比较两次得到的结果，如果结果相同，则说明该结果就是最优762刘晨，等：综合能源系统多能互补优化方法研究解，该策略为满足Nash均衡定义的最优策略。否则，会重复上述过程，直到找到最优策略。4实验分析4．1对象分析选取某小区作为实验对象来验证构建的博弈模型的有效性，用户的日逐时负荷作为纵坐标。模型中，用户的电、冷、热负荷会跟随一年四季而产生变化。全年分为：夏季、冬季和过渡季。根据图2（a）可知，在过渡季和冬季用电量差不多，在夏季的时候偏多。夏季的时候11∶00—22∶00期间对电负荷的需求开始增加，高峰期在12∶00—20∶00之间。由图2（b）可知，用户在夏季的对冷负荷会持续增长，在10∶00—20∶00期间会达到高峰，在过渡季较少用到冷负荷，而在冬季的时候几乎用不到冷负荷。由图2（c）可知，用户在冬季对热负荷的需求急剧增长，在11∶00—12∶00达到顶峰，后续就会慢慢减少，在过渡季和夏季的时候对热负荷需求不是很高。图2典型日逐时负荷4．2参数设定多能互补综合能源系统中配置的设备参数，如表2所示［19，27－30］。根据相关规定，假设小区分时电价为0．64元/（kW·h）［31－33］，热电联产用气价格为2．45元/Nm3［34］，资金投资年利率为5%［35－36］。表2设备性能参数参数数值热电联产的单位功率造价UC/（万元·kW－1）1．08热电联产的单位功率报废收入DC/（万元·kW－1）0．12热电联产的设备运维系数MC/（万元·（kW·h）－1）0．03热电联产的天然气气耗率V/（Nm3·（kW·h）－1）0．35热电联产机组热电比λ1．2热电联产使用寿命LC/a20换热器效率ηH/%80溴化锂吸收式制冷机性能系数COPC1．2电制冷机性能系数COPec4．7热泵性能系数COPH2．5光伏电池单位造价US/（万元·kW－1）0．6光伏电池使用寿命LS/a20光伏电池单位功率报废收入DS/（万元·kW－1）0．08光伏电池单位功率运维费用MS/（万元·（kW·h）－1）0．0164．3结果分析4．3．15种博弈结果分析综合能源系统在部分合作、完全合作和非合作模式下的均衡结果，如表3所示。Ptotal为系统总规划容量，Ptotal=HC+HＲ+HE；I为系统总收益；ΔI则为各合作博弈的联盟价值。由表3可知，5种博弈模式中，模式5可以让系统总收益变得最大，此时Nash均衡结果为（567，180，148），热电联产所占的容量比最大为63%，光伏发电次之为20%，电网最小为17%。模式1～模式5中，比较横向和纵向数据可862知，参与者容量均呈现HC＞HＲ＞HE的特性，热电联产可以作为全年的供能主体，光伏作为次供能，电网作为最小的供能体。当参与者采用非合作博弈模式时，产生的总体最低；采用完全合作博弈模式时，产生最大的整体效益；采用部分合作博弈模式时，产生的效益也相对偏低。4．3．2博弈收益分析由表3可知，系统的总收益在非合作博弈模式下会达到最低，在完全合作博弈模式下会达到最高。因此，系统更会倾向于合作博弈模式。表3博弈均衡结果模式编号博弈模式HC/kWHＲ/kWHE/kWPtotal/kWI/万元ΔI/万元1｛C｝，｛Ｒ｝，｛E｝6512431381032243．6302｛C，Ｒ｝，｛E｝54921387849301．5057．873｛C，E｝，｛Ｒ｝6853401271152254．8011．174｛E，Ｒ｝，｛C｝6943151061115273．1229．495｛C，Ｒ，E｝567180148895322．1678．53比较5种博弈模式的结果，最优模式是完全合作博弈，此时的最优容量是（567，180，148），总收益为322．16万元。与非合作博弈模式相比，完全合作博弈模式拥有着最大的系统收益和联盟收益。4．3．3供需平衡分析由上述可知，能源系统的最优模式是完全合作博弈模式，此时会产生最大的系统收益和联盟收益。为了使完全合作博弈模式更具有说服力，分析了夏季、冬季和过渡季3个典型日的电、冷、热负荷的供需平衡。由图3（a）可知，由于光伏电池的特性，只有在8∶00—16∶00时光伏电池才会产生电量，在12∶00—14∶00时刻产生的电量达到峰值，全天其余时刻的供电全依靠热电联产机组和电网供电，其中热电联产供能占比最大，超过一半以上，电网供电只会占据一小部分。由图3（b）和（c）可知，用户在夏季10∶00—20∶00时刻对冷负荷的需求急剧增加；在冬季10∶00—20∶00时刻对热负荷的需求急剧增加。图3供需平衡图962刘晨，等：综合能源系统多能互补优化方法研究5结论针对目前多能互补能源系统所存在设计、供需平衡以及系统利益差的问题，引入了经济学中的博弈论思想，以电网、热电联产和光伏发电作为参与者，求解系统的最大收益。比较了在非合作、部分合作和完全合作这3种博弈模式下的系统总收益。经过实验得知，在完全合作博弈下的系统总收益大于部分合作博弈和非合作博弈。验证了只有参与者完全进行合作，才能保证系统和联盟经济效益最大化。参考文献：［1］曹又敏．基于多能互补的园区综合能源系统优化调度［D］．西安：西安理工大学，2020．［2］PENGK，ZHANGC，XUB，etal．Statusandprospectofpilotprojectsofintegratedenergysystemwithmufti-ener-gycollaboration［J］．ElectricPowerAutomationEquip-ment，2017，37（61）：3－10．［3］JIANGXS，JINGZX，LIYZ，etal．Modellingandoper-ationoptimizationofanintegratedenergybaseddirectdistrictwater-heatingsystem［J］．Energy，2014，64：375－388．［4］DINGZX，JIANGXS，WUQH，etal．Modellingandoptimaloperationofasmall-scaleintegratedenergybaseddistrictheatingandcoolingsystem［J］．Energy，2014，73：399－415．［5］赵霞，杨仑，瞿小斌，等．电气综合能源系统能流计算的改进方法［J］．电工技术学报，2018，33（3）：467－477．［6］彭克，张聪，徐丙垠，等．多能协同综合能源系统示范工程现状与展望［J］．电力自动化设备，2017，37（6）：3－10．［7］李正茂，张峰，梁军，等．含电热联合系统的微电网运行优化［J］．中国电机工程学报，2015，35（14）：3569－3576．［8］陈沼宇，王丹，贾宏杰，等．考虑P2G多源储能型微网日前最优经济调度策略研究［J］．中国电机工程学报，2017，37（11）：3067－3077．［9］王珺，顾伟，陆帅，等．结合热网模型的多区域综合能源系统协同规划［J］．电力系统自动化，2016，40（15）：17－24．［10］刘洪，陈星屹，李吉峰，等．基于改进CPSO算法的区域电热综合能源系统经济调度［J］．电力自动化设备，2017，37（6）：193－200．［11］薛禹胜，雷兴，薛峰，等．关于风电不确定性对电力系统影响的评述［J］．中国电机工程学报，2014，38（29）：5029－5040．［12］张旭，梁军，负志皓，等．考虑风电接入不确定性的广义负荷建模及应用［J］．电力系统自动化，2014，38（20）：61－67．［13］FACCIAL，ANDＲEASSIL，UBEＲTINIS．OptimizationofCHCP（combinedheatpowerandcooling）systemsop-erationstrategyusingdynamicprogramming［J］．Energy，2014，66：387－400．［14］BISCHIA，TACCAＲIL，MAＲTELLIE，etal．AdetailedMILPoptimizationmodelforcombinedcooling，heatandpowersys-temoperationplanning［J］．Energy，2014，74：12－26．［15］BＲACCOS，DEONTICG，SIＲIS．Economicandenviron-mentaloptimizationmodelforthedesignandtheopera-tionofacombinedheatandpowerdistributedgenerationsysteminanurbanarea［J］．Energy，2013，55：1014－1024．［16］窦小敏，秦宁宁．电力系统经济调度的量子粒子群改进算法［J］．重庆邮电大学学报（自然科学版），32（4）：528－535．［17］任红波，侯亚群，李琦芬，等．基于博弈论的多能互补综合能源系统规划设计方法［J］．科学技术与工程，2021，21（5）：1812－1819．［18］陈建先．博弈理论框架：一个理论体系的建构［J］．重庆理工大学学报（社会科学），2018，32（1）：88－95．［19］任洪波，邓冬冬，吴琼，等．基于热电共融的区域分布式能源互联网协同优化研究［J］．中国电机工程学报，2018，38（14）：4023－4034，4308．［20］王锦桥．基于讨价还价博弈的分布式能源合作收益分配策略［D］．天津：天津大学，2018．［21］周亚蕾，于伟．基于工具理性和价值理性关系研究的技术选择［J］．技术与创新管理，2014，35（4）：405－408．［22］梅生伟，王莹莹，刘锋．风－光－储混合电力系统的博弈论规划模型与分析［J］．电力系统自动化，2011，35（20）：13－19．［23］林女贵，蔡冰凌，刘建．区域电网竞价策略研究［J］．电力需求侧管理，2019，21（2）：15－18，23．［24］柳高稳．函数凹凸性的概念及基本性质［J］．甘肃教育，2020（4）：187．［25］王海英，杨筱珊．拟凹函数的判别准则［J］．毕节学院学报，2010，28（8）：43－45．072［26］XUG，LIUY，KHANPW．ImprovementoftheDPoSconsensusmechanisminblockchainbasedonvaguesets［J］．IEEETransactionsonIndustrialInformatics，2020，16（6）：4252－4259．［27］周欣欣，刘魁星，刘书贤．应用于分布式能源系统的设备选择和容量配置模型［J］．热能动力工程，2019，34（7）：24－29．［28］张涛，朱彤，高乃平，等．分布式冷热电能源系统优化设计及多指标综合评价方法的研究［J］．中国电机工程学报，2015，35（14）：3706－3713．［29］梁浩，张峰，龙惟定．基于多能互补的区域能源系统优化模型［J］．暖通空调，2012，42（7）：60，67－71．［30］白海尚．小型分布式能源系统的优化研究［D］．太原：太原理工大学，2014．［31］国家发展和改革委员会，教育部．关于学校水电气价格有关问题的通知［EB/OL］．（2007－09－30）［2022－07－14］．https：//www．Ndrc．Gov．cn/xxgk/zcfb/tz/200709/t20070930_965466．html．［32］上海市物价局．上海市物价局关于进一步规范居民生活电价适用范围的通知［EB/OL］．（2015－12－01）［2022－07－14］．http：//fgw．sh．gov．cn/jgl/20151201/002517321．html．［33］上海市物价局．上海市发展改革委关于本市居民生活用电试行阶梯电价实施方案的通知［EB/OL］．（2012－06－14）［2022－07－14］．http：//fgw．sh．gov．cn/jgl/20120614/0025－17050．html．［34］上海市物价局．关于调整本市非居民用户天然气价格的通知［EB/OL］．（2019－14－30）［2022－07－14］．http：//fgw．Sh．Gov．cn/cxxxgk/20190430/0025－35829．html．［35］任洪波，王广涛，李琦芬，等．供需互动视角下区域综合能源系统设备配置与运行策略协同优化研究［J］．热力发电，2020，49（3）：60－67．［36］王惠，赵军，安青松，等．不同建筑负荷下分布式能源系统优化政策激励研究［J］．中国电机工程学报，2015，35（14）：3734－3740．Ｒesearchonmulti-energycomplementaryoptimizationmethodofintegratedenergysystemLIUChen1，LONGHao1，ZHANGWendong1，HUANGMeng2（1．WulingPowerCorporationLimited，Changsha410000，China；2．ShandongElectricPowerEngineeringConsultingInstituteCo．，Ltd．，Jinan250000，China）Abstract：Inviewofmycountry’senergysystemstructure，therearesomeproblemssuchaslowfunctionalefficiency，improperenergyallocation，andseriousenvironmentalpollution．Itisurgenttobuildanefficient，environmentallyandsafemulti-energycomplementaryintegratedenergysystem．Thegametheoryconceptisadoptedtorealizethemulti-energycomplementaryoptimaldispatchoftheintegratedenergysystemandoptimizesthetraditionalenergycoordinateddispatchproblem．Themodelconsistsofcogenerationunits，photovoltaicpowergeneration，andpowergrids．Themaximumbenefitsofthenon-cooperativegameandcooperativegamesolutionsystemareestablishedrespectively．Thetotalrevenuegeneratedbythesystemunderthethree-gamemodesofnon-cooperation，partialcooperationandfullcooperationiscomparedseparately．Accordingtowhethertheparticipant，sally，fivegamemodesareproposedtoprovetheNashequilibrium，andtheNashequilibriumstrategyineachmodeisobtainedthroughsimulationexperiments．Thesimulationresultsshowthat，comparedwithnon-cooperativegames，thevalueofothercooperativegamesisbetterthanthatofnon-cooperativegames，andthetotalprofitrateofthesystemunderthefullycooperativegamemodeisthelargest．Itisverifiedthatonlytheparticipantsfullycooperatetoensurethemaximizationoftheprofitofthemulti-energycomplementaryenergysystem．Keywords：gametheory；multi-energysystem；Nashequilibrium；cooperativegame；non-cooperativegame（责任编辑辛亮）172刘晨，等：综合能源系统多能互补优化方法研究